Results And Discussion Of Laplace Transform

Agustus 26, 2021 Posting Komentar

When it does the integral11issaidtoconvergeIfthelimitdoesnotexisttheintegral is said to diverge and there is no Laplace transform dened for f. Piere-Simon Laplace introduced a more general form of the Fourier Analysis that became known as the Laplace transform.

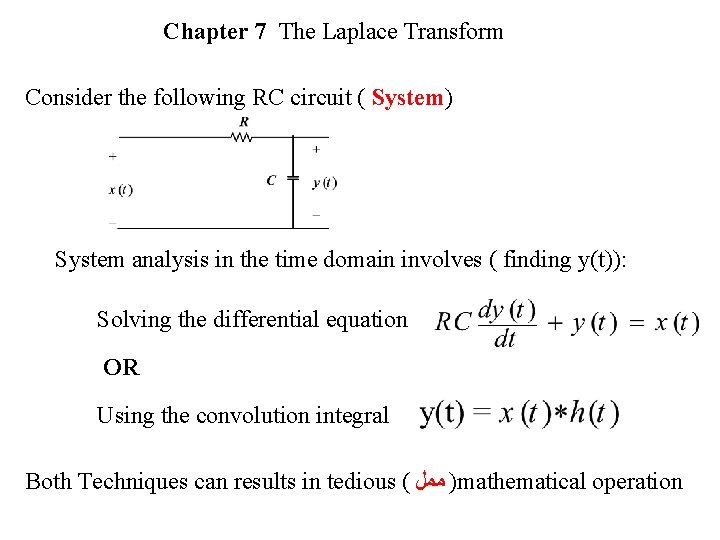
Chapter 7 The Laplace Transform Consider The Following

The causal version of the Fourier transform is the Laplace transform.

Results and discussion of laplace transform. You look at the table of common Laplace transforms to find a pattern and you see no rhyme no reason no obvious link between different functions and their different very different results. Like the Fourier transform the Laplace transform is used for solving differential and integral equations. If X is the random variable with probability density function say f then the Laplace transform of f is given as the expectation of.

It remains to invert L and recover v. Simplify algebraically the result to solve for Ly Ys in terms of s. Some mathematically oriented treatments of the unilateral Laplace transform such as 6 and 7 use the L form Lf.

We write f L1fFg. Engineering Mathematics with Examples and Solutions. We call ft the inverse Laplace transform of Fs Lfftg.

Laplace Transforms with Examples and Solutions. Find the inverse transform of Ys. To obtain the inverse transform of let us assume that Thus the following results can be obtained by the method in 14 17.

In our discussion the Laplace transform is chiefly used in control system analysis and design. In pure and applied probability theory the Laplace transform is defined as the expected value. Solve Differential Equations Using Laplace Transform.

In other words the Laplace transform can be thought of as the Fourier transform of a signal that has been modified by multiplying it by. The Duhamels principle Duhamel 183 3 used for solving. L 1 1 s a eat Example 2.

Depending upon the value of which is the real part of sthe signal. LfS Ee-sX which is referred to as the Laplace transform of. Laplace transforms are also important for process controls.

Therefore by imposing the Laplace transform on Eq. The Laplace transform on F NS now leads to fNSs LFNSs. This is in general a difficult task.

Xtcan be multiplied by a decaying or expanding exponential. It is made easy here by first recognizing that the factor 11 s in Eq. It aids in variable analysis which when altered produce the required results.

Let us take a moment to ponder how truly bizarre the Laplace transform is. 43 The Laplace Transform. Laplace transform should unambiguously specify how the origin is treated.

The process of solution consists of three main steps. Take the Laplace transforms of both sides of an equation. The Laplace transform of two con voluted fu nctions ft and gt yields the product of the transforms of the two functions.

L 1fc 1F 1s c 2F 2sg c 1 L 1fF 1sg c 2 L 1fF 2sg. The Laplace transform is related to the Fourier transform but whereas the Fourier transform expresses a function or signal as a series of modes of vibration frequencies the Laplace transform resolves a function into its moments. You put in a sine and get an oddly simple arbitrary-looking fractionWhy do we suddenly have squares.

Laplace transform of f as Fs L ft 0 estftdt lim 0 estftdt 11 whenever the limit exists as a nite number. Or rather find a function yt. 318 is itself the Laplace transform.

L 1 1 s an eat tn 1 n 1. The integral over time includes only positive values and hence only deals with causal impulse response functions 1. L 1 1 s2 b2 1 b sinbt.

It transforms a time-domain function ft into the s-plane by taking the integral of the function multiplied by e-st from 0- to infty where s is a complex number with the form ssigma jomega. The inverse Laplace transform is linear. We have expressed the Laplace transform of the response in terms of the Laplace transform of the stimulus.

The given hard problem is transformed into a simple equation. The Laplace transform can be used to solve di erential equations. The direct Laplace transform or the Laplace integral of a function.

To solve a linear differential equation using Laplace transforms there are only 3 basic steps. Apart from these two examples Laplace transforms are used in a lot of engineering applications and is a very useful method. 3 the result would be the.

An example of this can be found in experiments to do with heat. Basic De nitions and Results Laplace transform is yet another operational tool for solving constant coe -cients linear di erential equations. Where are functions specified by The inverse transform of which is the mode function of the pipe conveying fluid can be obtained as follows.

L 1 s s2 b2 cosbt Example 4. Be-sides being a di erent and e cient alternative to variation of parame-ters and undetermined coe cients the Laplace method is particularly advantageous for input terms that are piecewise-de ned periodic or im-pulsive. Formulas and Properties of Laplace Transform.

Inserting into yields where are defined by If the right of equation is the Dirac delta function the Green function of equation will be derived by. To understand and apply the unilateral Laplace transform students need to be taught an approach that addresses arbitrary inputs and initial conditions. On the other hand it is known that the Laplace transform of convolution factors will yield the ordinary product of the Laplace transform of those factors 30 35 36.

This simple equation is solved by purely algebraic. Inverse Laplace transform inprinciplewecanrecoverffromF via ft 1 2j Zj1 j1 Fsestds whereislargeenoughthatFs isdenedfor. Laplace Transforms Calculations Examples with Solutions.

Chapter 4 Laplace Transforms 4 Introduction 4 1